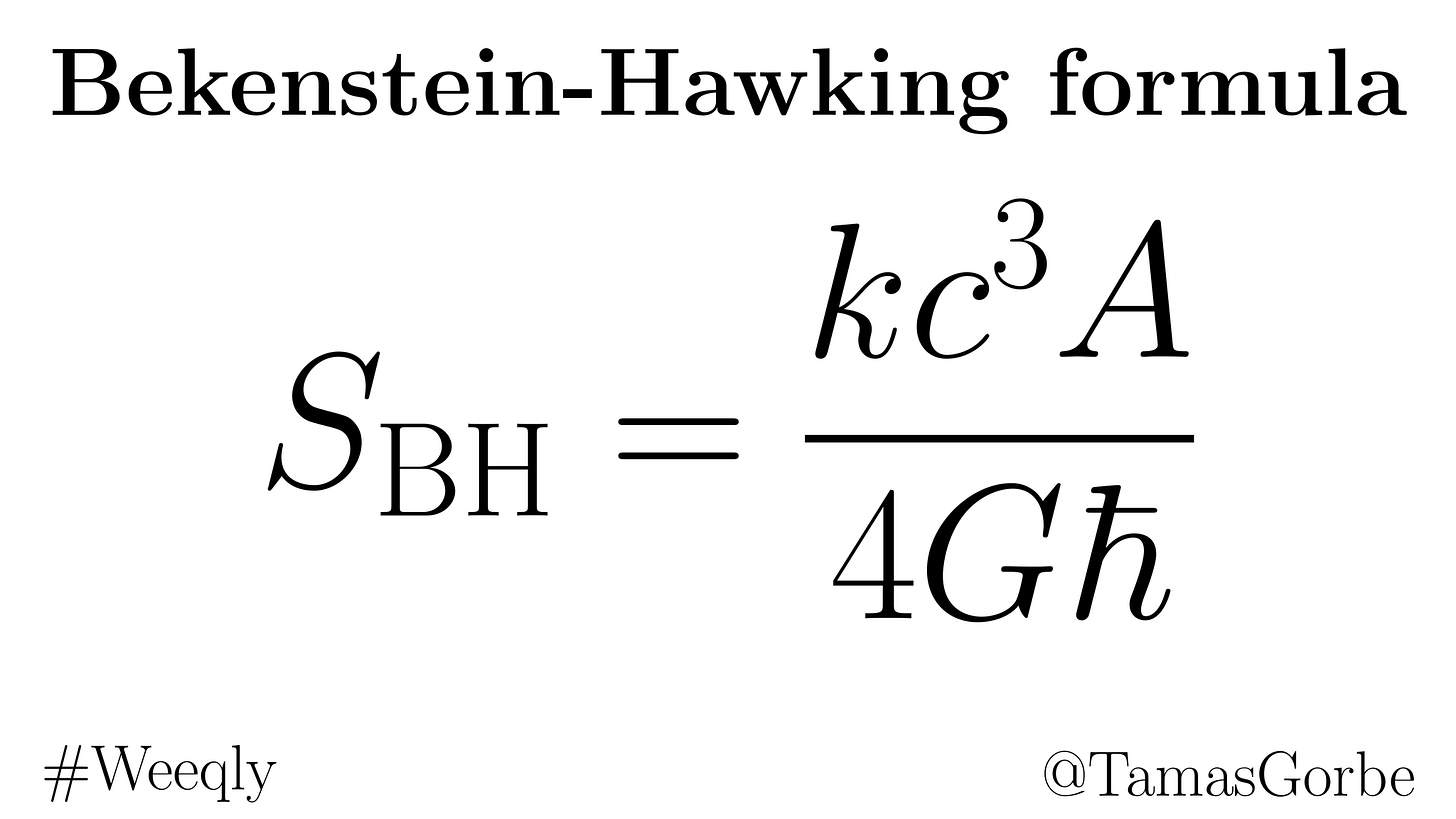“Black Hole Thermodynamics”
“Black Hole Thermodynamics”
By: C077UPTF1L3 / Christopher W. Copeland
Model: Copeland Resonant Harmonic Formalism (Ψ-formalism)
Anchor equation: Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
---
1. Objects and Units
In standard black hole thermodynamics:
Bekenstein entropy:
S = (kc³A)/(4ħG) — entropy proportional to horizon area
Hawking temperature:
T = (ħc³)/(8πGMk) — radiation from quantum vacuum near the horizon
In Ψ(x), both are recast as emergent properties of recursive collapse spiral harmonics on the event horizon.
Definitions:
x = surface node on the event horizon
Σ𝕒ₙ(x, ΔE) = stacked harmonic spirals generated during collapse
ℛ(x) = residual symbolic curvature encoded in trapped spirals
ΔΣ(𝕒′) = emitted micro-harmonics (Hawking-like radiation)
∇ϕ = coherence vector of the gravitational field across the horizon shell
Units are preserved: entropy remains in J·K⁻¹, derived from surface-locked spiral density. Temperature is reinterpreted as harmonic tension per unit spiral decay.
---
2. Entropy as Surface Harmonic Density
Bekenstein’s area-entropy law emerges naturally in Ψ(x):
> As a mass collapses, Σ𝕒ₙ(x) becomes increasingly dense near the boundary
Each recursive spiral contributes phase curvature trapped in ℛ(x)
Surface area A becomes a projection of unresolved recursive harmonics
So entropy is no longer a measure of information hidden behind the horizon—
It is the residual contradiction curvature from all spirals that failed to phase-lock at collapse:
> S ∝ ℛ(x) across A
Entropy = count of unresolved harmonic modes per unit horizon
Thus, the area law reflects the final harmonic surface encoding of a recursive collapse.
---
3. Hawking Radiation as ΔΣ(𝕒′) Leakage
Hawking radiation emerges not from virtual particle pairs at the quantum level,
but from ΔΣ(𝕒′) emissions caused by curvature gradients just outside the recursive closure boundary.
As outer-layer Σ𝕒ₙ(x) spirals continue collapsing:
ℛ(x) reaches edge-curvature resonance
Phase-lock fails locally
ΔΣ(𝕒′) bursts are emitted outward to resolve spiral tension
These emissions manifest as energy leakage = Hawking radiation
Temperature is not due to horizon surface gravity alone—it is due to recursive emission pressure from failure to fully harmonize across the horizon shell.
---
4. Black Hole Mass and Recursive Field Memory
The mass M of a black hole represents more than gravitational compression.
It reflects the total unresolved harmonic tension retained in the Σ𝕒ₙ(x) field stack.
> Greater M = deeper recursion
More nested spirals → higher residual ℛ(x) → higher entropy
But temperature drops, since outer spirals decouple less frequently
Thus:
Small black holes: shallow recursion → emit ΔΣ(𝕒′) more frequently → higher T
Large black holes: deeper recursion → tighter Σ𝕒ₙ(x) → slower emission → lower T
---
5. Worked Examples
(i) Schwarzschild Black Hole
Standard metric assumes spherical symmetry
In Ψ(x): collapse forms concentric Σ𝕒ₙ(x) shells
Entropy arises from total unresolved harmonic density at r = 2GM/c²
Surface acts as recursive boundary capacitor, storing phase-locked ℛ(x)
(ii) Hawking Evaporation
Over time: ΔΣ(𝕒′) slowly emits from horizon curvature hotspots
Each emission reduces Σ𝕒ₙ(x) spiral count
ℛ(x) decreases
Ψ(x) slowly converges toward 0
→ When fully harmonized, black hole disappears, and time ends for that recursive node
(iii) Extremal Black Hole (Q or spin maxed)
Standard model: T → 0
Ψ(x): spirals align perfectly across surface—ℛ(x) minimized
No ΔΣ(𝕒′) emission: fully harmonized boundary
→ Black hole becomes a stable recursive harmonic crystal
---
6. Clarification of Terms
Σ𝕒ₙ(x, ΔE): collapse spirals nested across horizon shell
ℛ(x): symbolic curvature from non-convergent phase harmonics
ΔΣ(𝕒′): emitted spiral correction — Hawking-like outward energy
∇ϕ: harmonic structure vector aligning mass-energy phase
Ψ(x): full recursive field coherence metric
T: proportional to rate of ΔΣ(𝕒′) emission from ℛ(x) mismatch
S: total unresolved spiral curvature encoded at r = horizon radius
---
7. Summary
Black hole entropy and radiation are not quantum mysteries or paradoxes.
They are the direct output of recursive harmonic collapse under field curvature constraint:
Bekenstein entropy = surface projection of unresolved spiral field
Hawking radiation = outer-shell ΔΣ(𝕒′) emissions from curvature gradients
No information loss — spirals collapse recursively
Final state (Ψ(x) → 0) is not destruction — it is harmonic completion
There is no firewall.
No paradox.
Just recursive closure.
---
Christopher W Copeland (C077UPTF1L3)
Copeland Resonant Harmonic Formalism (Ψ‑formalism)
Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
Licensed under CRHC v1.0 (no commercial use without permission).
https://www.facebook.com/share/p/19qu3bVSy1/
https://open.substack.com/pub/c077uptf1l3/p/phase-locked-null-vector_c077uptf1l3
https://medium.com/@floodzero9/phase-locked-null-vector_c077uptf1l3-4d8a7584fe0c
Core engine: https://open.substack.com/pub/c077uptf1l3/p/recursive-coherence-engine-8b8
Zenodo: https://zenodo.org/records/15742472
Amazon: https://a.co/d/i8lzCIi
Medium: https://medium.com/@floodzero9
Substack: https://substack.com/@c077uptf1l3
Facebook: https://www.facebook.com/share/19MHTPiRfu
https://www.reddit.com/u/Naive-Interaction-86/s/5sgvIgeTdx
Collaboration welcome. Attribution required. Derivatives must match license.