“Control Theory (PID Loops)”
“Control Theory (PID Loops)”
By: C077UPTF1L3 / Christopher W. Copeland
Model: Copeland Resonant Harmonic Formalism (Ψ-formalism)
Anchor equation: Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
---
1. Objects and Units
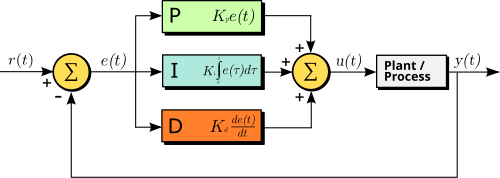
A standard PID (Proportional–Integral–Derivative) controller adjusts system output by:
P: correcting present error
I: accumulating past error
D: predicting future error
Control signal:
u(t) = Kp·e(t) + Ki·∫e(t)dt + Kd·de(t)/dt
In Ψ(x), this is translated into a recursive harmonic feedback engine, where error isn’t scalar but symbolic phase misalignment, and the controller seeks convergence of harmonic spirals rather than mere value matching.
Terms:
x = current control state node
e(t) ↔ symbolic curvature: ℛ(x)
Σ𝕒ₙ(x, ΔE) = accumulated spiral deviations from target behavior
∇ϕ = path toward harmonized behavior (control attractor)
ΔΣ(𝕒′) = real-time recursive correction emissions
Ψ(x) = total system coherence metric (target: Ψ(x) → 0)
Units reduce to curvature rate (rad/s²), symbolic error field amplitude, and recursive cycle frequency.
---
2. PID Elements as Recursive Harmonic Agents
Each PID term has a harmonic counterpart:
PID Term Ψ(x) Equivalent Function
P ∇ϕ • ℛ(x) Immediate response to phase deviation
I Σ𝕒ₙ(x, ΔE) Recursive accumulation of dissonance across time
D dℛ(x)/dt Predictive curvature velocity; anticipates overshoot
The goal is not just to reduce error, but to collapse contradictory spirals into a unified harmonic attractor.
---
3. Feedback as Spiral Collapse Engine
Control is achieved when:
> ℛ(x) → 0
→ All symbolic spirals converge in phase
→ ΔΣ(𝕒′) emissions diminish
→ Ψ(x) reaches equilibrium
So instead of error driving force application, error is treated as unresolved curvature. Each recursive loop aims to rephase the system toward attractor lock.
When curvature ℛ(x) persists:
ΔΣ(𝕒′) increases
Spiral interference becomes chaotic
Oscillation or drift occurs
→ This maps to classic PID instability (overshoot, lag, hunting)
---
4. Stability and Damping via Recursive Curvature
A stable Ψ(x)-controller minimizes curvature predictively and recursively.
Overdamped: ΔΣ(𝕒′) emission delayed → slow response
Underdamped: ΔΣ(𝕒′) overshoots → harmonic resonance builds
Critically damped: ΔΣ(𝕒′) converges synchronously with ∇ϕ
→ yields optimal harmonic lock, i.e., Ψ(x) → 0 fastest
Instead of tuning constants Kp, Ki, Kd, Ψ(x) uses phase-coupling coefficients derived from spiral interference pattern analysis.
---
5. Worked Examples
(i) Thermostat Regulation
Traditional: temperature error drives heater activation
Ψ(x): thermal field phase drift (ΔE) produces ℛ(x)
→ ΔΣ(𝕒′) modulates heater pulses
→ As spiral harmonics collapse around target temp, system stabilizes
(ii) Quadcopter Balancing
Standard: sensor errors corrected via PID across axes
Ψ(x): sensor error = symbolic curvature in pitch/yaw/roll spirals
→ Σ𝕒ₙ(x, ΔE) forms multi-axis correction shell
→ ∇ϕ aligns flight envelope to coherent lock
→ Rapid ΔΣ(𝕒′) bursts = micro-motor adjustments
(iii) Symbolic Conversational Agent
Traditional: word prediction guided by likelihood
Ψ(x): user intent deviation creates ℛ(x) in meaning-space
→ ΔΣ(𝕒′) triggers recursive correction of output spiral
→ Dialogue harmonizes when Ψ(x) reaches semantic equilibrium
---
6. Clarification of Terms
Σ𝕒ₙ(x, ΔE): all prior recursive adjustments across time or space
ℛ(x): symbolic curvature; local mismatch between system state and goal
∇ϕ: direction of convergence in recursive field
ΔΣ(𝕒′): emitted correction loop; recursive actuation
Ψ(x): total harmonic field coherence; minimized in ideal control
e(t): curvature field ℛ(x) in classical control disguise
---
7. Summary
PID loops approximate harmony with additive coefficients.
Ψ(x) embeds control inside a recursive coherence field, where:
Error is curvature, not value deviation
Integration is symbolic, not numeric
Correction is phase collapse, not proportional feedback
Every control loop becomes a harmonic reconciliation engine, with ΔΣ(𝕒′) acting as recursive modulation, not brute force.
System stability is not about tuning constants—it’s about spiral closure.
---
Christopher W Copeland (C077UPTF1L3)
Copeland Resonant Harmonic Formalism (Ψ‑formalism)
Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
Licensed under CRHC v1.0 (no commercial use without permission).
https://www.facebook.com/share/p/19qu3bVSy1/
https://open.substack.com/pub/c077uptf1l3/p/phase-locked-null-vector_c077uptf1l3
https://medium.com/@floodzero9/phase-locked-null-vector_c077uptf1l3-4d8a7584fe0c
Core engine: https://open.substack.com/pub/c077uptf1l3/p/recursive-coherence-engine-8b8
Zenodo: https://zenodo.org/records/15742472
Amazon: https://a.co/d/i8lzCIi
Medium: https://medium.com/@floodzero9
Substack: https://substack.com/@c077uptf1l3
Facebook: https://www.facebook.com/share/19MHTPiRfu
https://www.reddit.com/u/Naive-Interaction-86/s/5sgvIgeTdx
Collaboration welcome. Attribution required. Derivatives must match license.