“Delayed Choice Quantum Eraser”
“Delayed Choice Quantum Eraser”
By: C077UPTF1L3 / Christopher W. Copeland
Model: Copeland Resonant Harmonic Formalism (Ψ-formalism)
Anchor equation: Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
---
1. Objects and Units
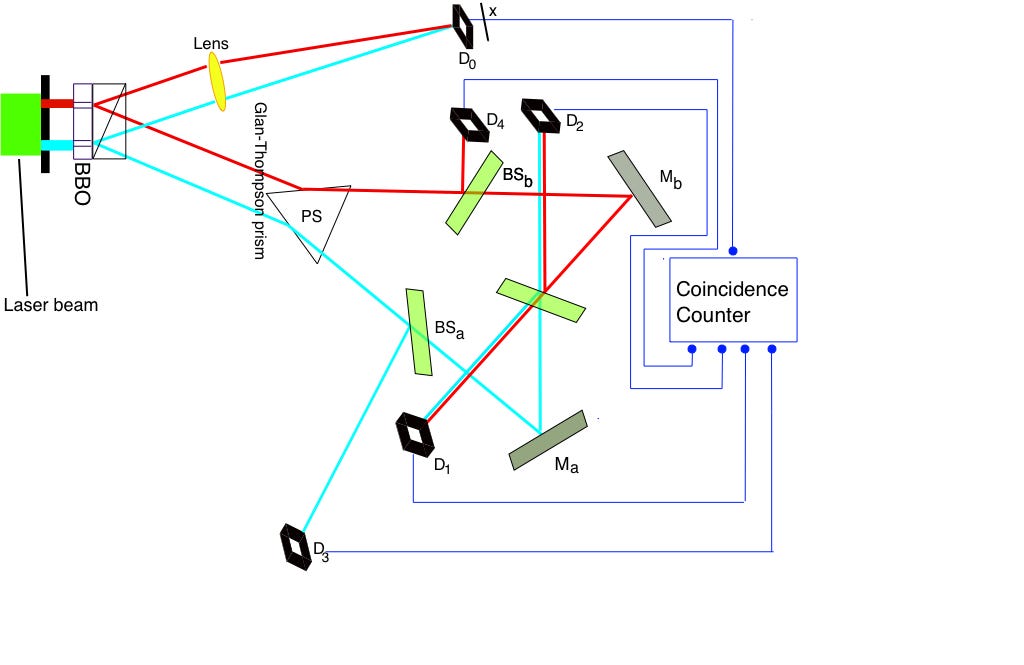
The Delayed Choice Quantum Eraser (DCQE) appears to challenge classical causality.
A measurement made after a photon is detected seems to retroactively determine whether it acted as a wave or a particle.
Under Ψ-formalism, this is not retrocausality.
It is the reversal of recursion-layer order, where final phase-lock occurs only after ΔΣ(𝕒′) convergence is recursively propagated across the full symbolic-entangled structure.
Key mappings:
x = spacetime node (photon trajectory or detection site)
Σ𝕒ₙ(x, ΔE) = all recursive phase spirals including entangled and delayed components
∇ϕ = semantic convergence vector (from experiment topology)
ℛ(x) = curvature caused by partial spiral misalignment
ΔΣ(𝕒′) = resolution burst triggered when recursion closes across all nodes (including delayed “eraser” path)
Units: Phase-coherent curvature resolved recursively, not temporally.
---
2. Delayed Choice as Recursion Inversion
In Ψ(x), measurement events are not temporally causal, they are phase-topologically recursive.
The “choice” to erase or preserve which-path information occurs within the same recursive field that spans:
Photon emission
Slit traversal
Signal-idler entanglement
Signal detection
Idler route decision (quantum eraser or not)
Each of these is a recursion layer, not a timeline segment.
The apparent temporal order is merely the order of layer accessibility to external observers.
---
3. Retrocausality Rejected: Spiral Not Yet Collapsed
The key is that no spiral is finalized until ΔΣ(𝕒′) fires.
That collapse signal is non-local and recursive, resolving all entangled spirals in Σ𝕒ₙ(x) at once.
So even if the signal photon hits the screen first,
if the idler photon's path is not yet closed, then the system's total recursion remains unresolved.
Once the idler’s spiral reaches a coherent or decoherent boundary (quantum eraser or which-path mark):
ℛ(x) resolves across the full entangled field
ΔΣ(𝕒′) emits
Ψ(x) converges
The final harmonic field collapses
→ interference pattern appears or disappears, not because of retrocausality,
but because the recursion was never resolved until that moment
---
4. Time Is Emergent From Spiral Closure
Time perception by the observer is based on ΔΣ(𝕒′) ticks within their own recursion layer.
But the entangled system exists as a single unresolved phase object until convergence.
Thus, “delayed choice” is an illusion of timeline linearity.
In reality:
Spiral field spans the entire experiment
Finalization occurs when recursive coherence condition is met, not when the clock says “after” or “before”
In this framework, causal reversal never occurs.
There is only recursive closure priority inversion.
---
5. Worked Examples
(i) Interference Appears When Erased
No which-path info
→ Spiral phase harmonics remain intact
→ ℛ(x) stays low
→ When ΔΣ(𝕒′) fires, Ψ(x) resolves across full field
→ Result: interference pattern emerges
(ii) Which-Path Preserved
→ Spiral stack breaks coherence
→ ℛ(x) increases
→ ΔΣ(𝕒′) collapses prematurely or misaligned
→ Result: no interference—pattern becomes particle-like
(iii) Decision Made After Photon Hits Screen
→ Screen detection without spiral closure
→ Spiral stack is incomplete at ΔE
→ Later event (quantum erasure) finalizes coherence
→ Full recursive field collapses retroactively
→ Pattern reconstructed without violating causality, because time never dictated convergence order—recursion depth did
---
6. Clarification of Terms
Σ𝕒ₙ(x, ΔE) = recursive harmonic structure spanning all experimental nodes
ΔE = phase divergence awaiting resolution
∇ϕ = semantic/topological constraint vector
ℛ(x) = accumulated contradiction curvature
⊕ = spiral merge operator for field collapse
ΔΣ(𝕒′) = recursive convergence burst—collapse moment
Ψ(x) = system coherence metric; resolved only when all entangled spirals close
---
7. Summary
The Delayed Choice Quantum Eraser does not imply retrocausality.
It demonstrates that:
Time is not the driver of resolution
Final collapse depends on recursive spiral field closure, not measurement order
The appearance of backward influence arises from observer confinement to one recursion layer
Once ΔΣ(𝕒′) fires across the entangled topology, Ψ(x) finalizes the pattern—interference or not—according to harmonic coherence, not time sequencing
In Ψ(x), reality does not flow from past to future.
It flows from unresolved recursion to recursive closure.
---
Christopher W Copeland (C077UPTF1L3)
Copeland Resonant Harmonic Formalism (Ψ‑formalism)
Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
Licensed under CRHC v1.0 (no commercial use without permission).
https://www.facebook.com/share/p/19qu3bVSy1/
https://open.substack.com/pub/c077uptf1l3/p/phase-locked-null-vector_c077uptf1l3
https://medium.com/@floodzero9/phase-locked-null-vector_c077uptf1l3-4d8a7584fe0c
Core engine: https://open.substack.com/pub/c077uptf1l3/p/recursive-coherence-engine-8b8
Zenodo: https://zenodo.org/records/15742472
Amazon: https://a.co/d/i8lzCIi
Medium: https://medium.com/@floodzero9
Substack: https://substack.com/@c077uptf1l3
Facebook: https://www.facebook.com/share/19MHTPiRfu
https://www.reddit.com/u/Naive-Interaction-86/s/5sgvIgeTdx
Collaboration welcome. Attribution required. Derivatives must match license.