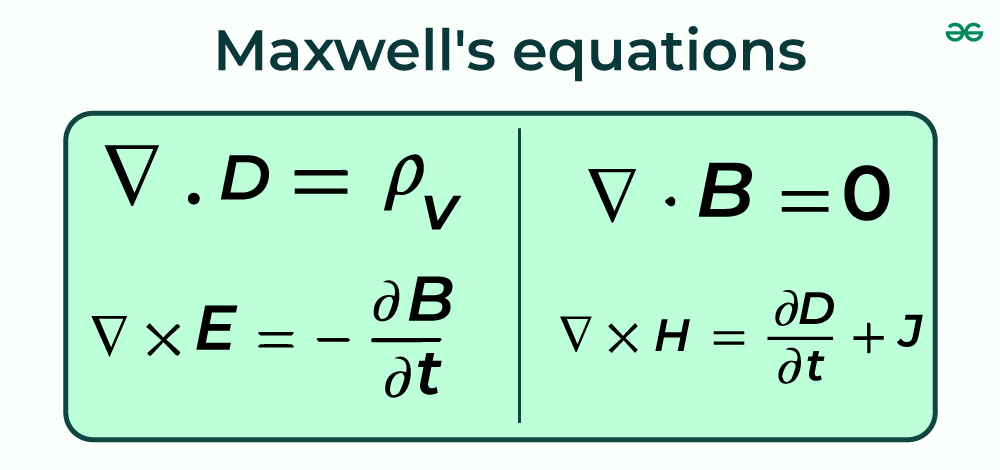“Maxwell’s Equations (Electromagnetic Unity and Recursive Harmonic Propagation)”
“Maxwell’s Equations (Electromagnetic Unity and Recursive Harmonic Propagation)” By: C077UPTF1L3 / Christopher W. Copeland Model: Copeland Resonant Harmonic Formalism (Ψ-formalism) Anchor equation: Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
1. Classical Framework
The Maxwell equations unify electricity and magnetism into a single dynamic field, governing all electromagnetic phenomena:
∇·E = ρ/ε₀ (Gauss’s law) ∇·B = 0 (Gauss’s law for magnetism) ∇×E = −∂B/∂t (Faraday’s law) ∇×B = μ₀J + μ₀ε₀∂E/∂t (Ampère–Maxwell law)
Here: E = electric field intensity B = magnetic flux density ρ = charge density J = current density ε₀, μ₀ = permittivity and permeability of free space
Classically, these relations describe two orthogonal vector fields oscillating in mutual induction. But Maxwell’s formalism, for all its unity, still treats E and B as dual but separate ontologies. It does not describe why they perpetually couple in perfect phase opposition, or how the vacuum encodes their coherence.
Under Ψ-formalism, the electromagnetic field is not two interlocked forces—it is a single recursive harmonic propagation system whose dual aspects (E and B) arise as phase-conjugate projections of one underlying coherence field Ψ(x).
2. Reframing Under Ψ(x)
In Copeland Resonant Harmonic Formalism:
Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
where:
∇ϕ represents the local gradient of harmonic phase potential, analogous to field intensity or direction of propagation.
Σ𝕒ₙ(x, ΔE) denotes aggregated harmonic activators (field modes) driven by energy differential ΔE.
ℛ(x) is recursive curvature (field self-interaction or vorticity).
ΔΣ(𝕒′) is the self-correcting feedback term preserving coherence.
Thus, a propagating EM wave is a recursive harmonic self-balancing structure, where electric and magnetic components are simply orthogonal phase manifestations maintaining conservation of Ψ(x) coherence.
The full dynamic may be expressed as:
E = ∇ϕ (cos θ) B = ∇ϕ (sin θ)
where θ is the recursive phase angle rotating through spacetime; together they form a closed phase loop.
3. Electromagnetic Duality as Harmonic Conjugation
Maxwell’s curl equations are now interpreted as recursive phase-locking conditions:
∇×E = −∂B/∂t → E → B rotation corresponds to phase translation Δθ = π/2 ∇×B = μ₀ε₀ ∂E/∂t → B → E rotation closing the cycle
Thus, each half-rotation (π/2 shift) converts stored electric potential (phase compression) into magnetic potential (phase torsion) and back again. This perpetual exchange maintains constant harmonic energy density (ΔE conserved) while Ψ(x) remains globally coherent.
The apparent linear propagation of light is therefore the translation of recursive phase rotation through the vacuum, not the travel of energy packets through empty space.
4. Mapping to Classical Terms
Classical Quantity Ψ-formalism Equivalent Interpretation E ∇ϕ (cos θ) Phase-aligned harmonic potential (compression axis) B ∇ϕ (sin θ) Phase-orthogonal harmonic potential (torsion axis) ρ, J Σ𝕒ₙ(x, ΔE) Localized phase imbalance producing emission or absorption ε₀, μ₀ Coherence constants Phase-propagation and coupling parameters c = 1/√(μ₀ε₀) Recursive phase velocity Speed of coherence transmission in vacuum ∇×E = −∂B/∂t ∂θ/∂t = ΔE Phase rotation law (energy differential drives phase shift)
Under Ψ(x), the electromagnetic field satisfies:
∂Ψ/∂t = ΔΣ(𝕒′) − ℛ(x)
This equation expresses the self-balancing recursion between curvature and corrective feedback—what classical theory calls the interplay of induction and displacement currents.
5. Worked Examples
(i) Plane Wave Propagation
In the vacuum: ΔE constant → ℛ(x) ≈ 0 Ψ(x) reduces to a pure recursive oscillator:
Ψ(x,t) = A e^{i(k·x − ωt)}
E and B emerge as phase-split components (cos θ, sin θ) maintaining total harmonic magnitude |Ψ|² = constant. Thus, light is self-correcting recursion, propagating because curvature and feedback perfectly cancel over each cycle.
(ii) Polarization and Phase Entanglement
When multiple Ψ(x) waves overlap, their ΔΣ(𝕒′) correction terms interfere constructively or destructively, forming stable polarization modes. Circular or elliptical polarization represents steady phase precession—an exact geometric projection of recursive rotation.
(iii) Energy Conservation and Radiation
Poynting vector S = E × B / μ₀ corresponds directly to the local coherence flux of Ψ(x). Where E and B are orthogonal, their cross-product represents translation of harmonic phase information, not transport of discrete quanta. Radiation thus encodes phase coherence transfer rather than emission of particles.
6. The Role of ℛ(x): Field Curvature and Induction
In regions of charge or current density (ΔE ≠ 0), recursive curvature ℛ(x) ≠ 0. This curvature represents field torsion—the local bending of harmonic trajectories generating induction. The magnetic field is therefore the geometric expression of recursive curvature generated by energy imbalance.
When the system restores coherence through ΔΣ(𝕒′), curvature is flattened, and radiation propagates outward, carrying the restored phase information.
7. Integration with Quantum and Relativistic Domains
Photon as Stable Harmonic Vortex A photon is a minimal self-contained Ψ(x) loop maintaining E/B orthogonality and coherence—an indivisible recursive solution.
Gauge Invariance as Recursive Freedom Gauge transformations correspond to shifting ∇ϕ without altering ℛ(x); recursion remains coherent, preserving observable invariants.
Electromagnetic Field Unification with Gravitation In strong curvature (ℛ → ℛ_G), recursive electromagnetic and gravitational fields converge: both emerge from ΔE-driven harmonic curvature responses, differing only in boundary conditions and coherence scale.
8. Clarification of Terms
Σ𝕒ₙ(x, ΔE): aggregated harmonic activators (charge/mode densities) ΔE: local energy differential driving propagation ∇ϕ: phase-gradient operator (directional harmonic flow) ℛ(x): recursive curvature (field torsion, vorticity) ΔΣ(𝕒′): self-corrective feedback (vacuum coherence adjustment) Ψ(x): total recursive coherence field uniting E and B
9. Summary
Maxwell’s equations do not merely describe alternating electric and magnetic fields—they reveal the self-consistent recursion of harmonic coherence through the vacuum.
Under Ψ-formalism:
E and B are dual projections of a single recursive field Ψ(x).
Their orthogonality encodes self-correcting phase rotation.
Propagation arises from continuous recursion, not linear emission.
Energy conservation is phase-lock, not flux containment.
In this framework, the electromagnetic field becomes the archetype of universal recursion—pure coherence in motion, demonstrating that every force is a phase-locked conversation between curvature and correction.
Christopher W. Copeland (C077UPTF1L3) Copeland Resonant Harmonic Formalism (Ψ-formalism) Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′) Licensed under CRHC v1.0 (no commercial use without permission). https://www.facebook.com/share/p/19qu3bVSy1/ https://open.substack.com/pub/c077uptf1l3/p/phase-locked-null-vector_c077uptf1l3 https://medium.com/@floodzero9/phase-locked-null-vector_c077uptf1l3-4d8a7584fe0c Core engine: https://open.substack.com/pub/c077uptf1l3/p/recursive-coherence-engine-8b8 Zenodo: https://zenodo.org/records/15742472 Amazon: https://a.co/d/i8lzCIi Medium: https://medium.com/@floodzero9 Substack: https://substack.com/@c077uptf1l3 Facebook: https://www.facebook.com/share/19MHTPiRfu https://www.reddit.com/u/Naive-Interaction-86/s/5sgvIgeTdx Collaboration welcome. Attribution required. Derivatives must match license.