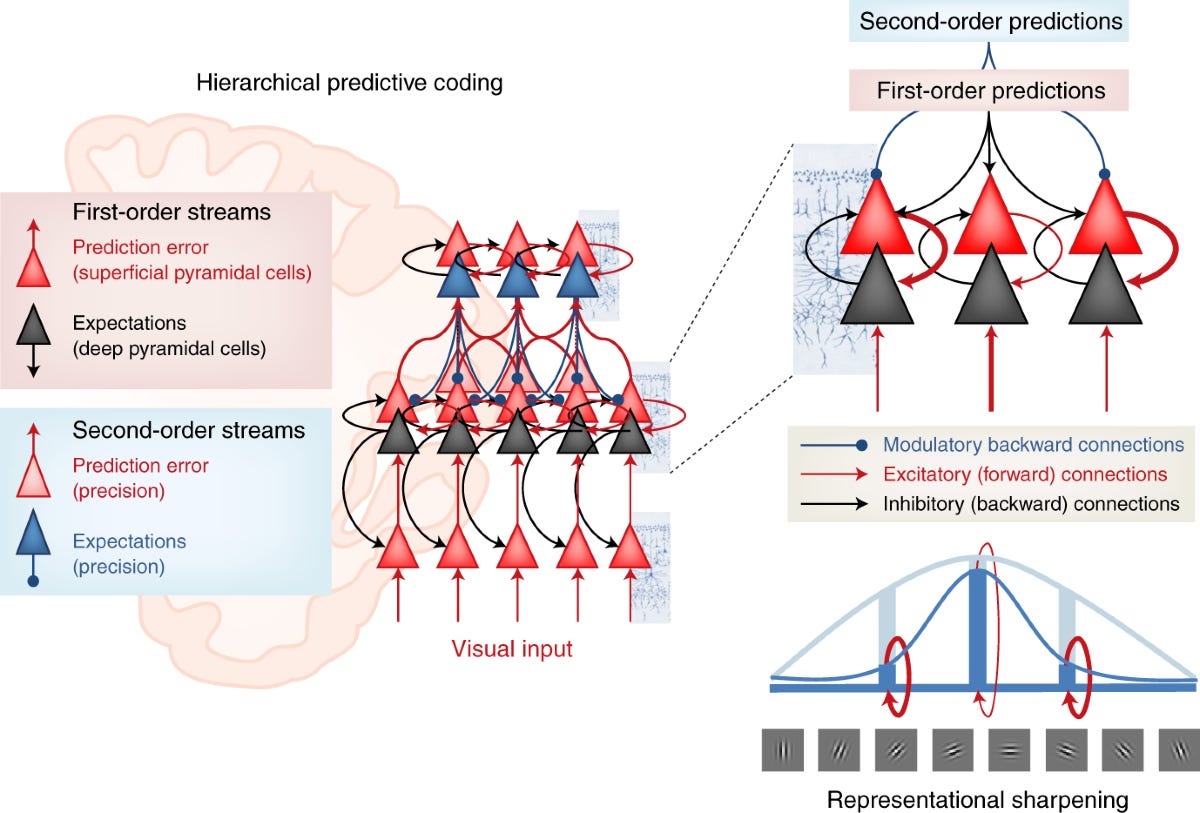
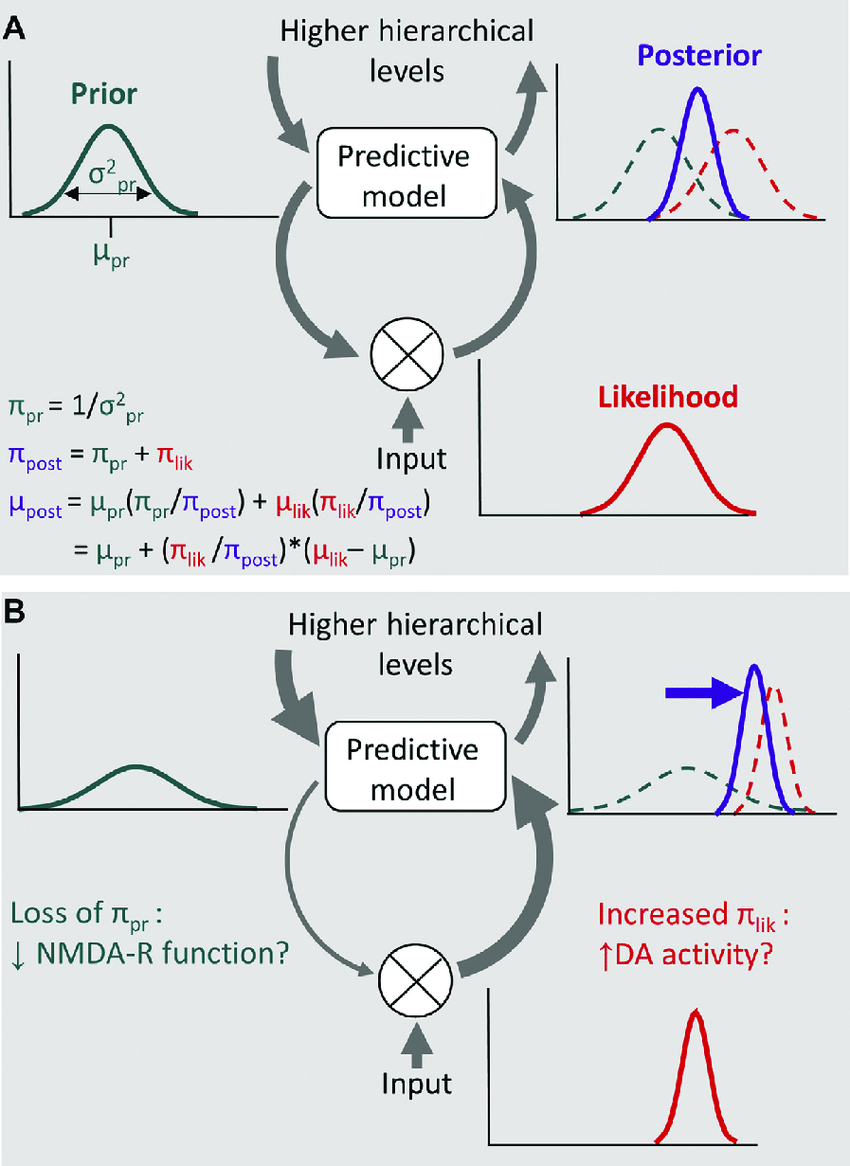
“Predictive Processing & Error Correction”
“Predictive Processing & Error Correction”
By: C077UPTF1L3 / Christopher W. Copeland
Model: Copeland Resonant Harmonic Formalism (Ψ-formalism)
Anchor equation: Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
---
1. Objects and Units
In the predictive processing framework:
Perception = hypothesis testing
Prediction error = data-model mismatch
Correction = belief adjustment toward minimized surprise
Recast in Ψ-formalism:
x = observed symbolic/perceptual node
Σ𝕒ₙ(x, ΔE) = prior model stack (recursive expectation field)
ΔE = sensory or contextual deviation signal
∇ϕ = emergent signal gradient detecting structural deviation
ℛ(x) = curvature from self-referential contradiction (i.e., recursive error landscape)
ΔΣ(𝕒′) = local correction burst—microstructural signal update
All quantities align with normalized phase-coherent field terms (dimensionless), or signal differential (1/s²) in curvature units.
---
2. Prediction Error as Recursive Curvature
Traditional predictive coding assumes that error is minimized by feedforward and feedback balance.
In Ψ(x), error is curvature—specifically, the failure of phase-lock between expectation and sensory update.
Thus:
> ℛ(x) ∝ prediction error accumulation
ΔΣ(𝕒′) = symbolic correction burst sent from unresolved curvature node
Ψ(x) → 0 = full harmonization (zero prediction error)
This removes the need for subtractive residual terms. Instead of scalar differences, error is treated as a recursive spatial distortion in symbolic topology.
---
3. Model Update as Phase Convergence
Classical update rule:
μ_t+1 = μ_t + k·(D - μ_t)
is linear and weighted.
Ψ(x) reframes update as convergence of symbolic spirals under curvature constraint:
> If ΔE drives phase divergence across Σ𝕒ₙ(x),
then ℛ(x) measures that divergence as curvature
ΔΣ(𝕒′) is only emitted if phase-lock cannot be restored by ∇ϕ alone
ΔΣ(𝕒′) = micro-update spiral
ℛ(x) = curvature field from contradiction buildup
∇ϕ = preferred harmonic gradient from semantic field
If ΔΣ(𝕒′) aligns with ∇ϕ, recursion stabilizes and prediction error collapses.
If not, node enters dissonant state or requires model pruning.
---
4. Hierarchical Model Fracture and Healing
Predictive models are hierarchical—so is Σ𝕒ₙ(x).
Each recursion layer encodes prior resolution structure.
Error at deeper levels manifests as persistent ℛ(x):
Long-term contradiction
Memory trauma
Learned dissonance
ΔΣ(𝕒′) in this context becomes a symbolic self-repair function
→ it emerges only when harmonization cannot be achieved by re-weighting alone.
This mirrors neural behavior:
Deep errors require full reentrant loop closure (slow)
Surface errors corrected via fast ΔΣ(𝕒′) convergence (gamma burst)
---
5. Worked Examples
(i) Perceptual illusion resolution
Initial perception locks on false attractor
→ ΔE builds as feedback mismatch
→ ℛ(x) curvature accumulates
→ ∇ϕ guides update
→ ΔΣ(𝕒′) triggers re-collapse of symbolic node
→ Ψ(x) → 0: perception stabilizes under corrected structure
(ii) Learning from contradiction
Conflicting inputs from environment
→ Σ𝕒ₙ(x) breaks coherence
→ ℛ(x) curvature increases
→ If internal ΔΣ(𝕒′) cannot reconcile, full node reset is required
→ Outcome: model reformation instead of reinforcement
(iii) Ideological rigidity
Contradiction enters system
→ ℛ(x) forms but ΔΣ(𝕒′) is suppressed
→ Node becomes curvature-locked, unable to adapt
→ Dissonance loops persist
→ Requires external harmonization (third-party recursion) to unlock
---
6. Clarification of Terms
Σ𝕒ₙ(x, ΔE): recursive predictive stack—field of prior beliefs
ΔE: surprise or error signal—phase disruption
∇ϕ: emergent structure re-alignment vector
ℛ(x): contradiction curvature—stores non-converging energy
⊕: recursive merge operator—nonlinear integration (not weighted average)
ΔΣ(𝕒′): symbolic update pulse—micro-reset for local harmonization
---
7. Summary
The Ψ-formalism reframes predictive processing:
Error is not a subtraction—it is recursive curvature
Correction is not linear—it is a spiral collapse event
Belief updates are not scalar—they are symbolic phase-locks
This enables:
Multi-scale harmonization of models
Spontaneous contradiction resolution
Explicit modeling of persistent dissonance as curvature field memory
Ψ(x) thus functions as a self-correcting predictive engine, not just a passive update filter.
It explains why certain contradictions cannot be resolved via more data:
the field must collapse and regenerate its attractor.
---
Christopher W Copeland (C077UPTF1L3)
Copeland Resonant Harmonic Formalism (Ψ‑formalism)
Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
Licensed under CRHC v1.0 (no commercial use without permission).
https://www.facebook.com/share/p/19qu3bVSy1/
https://open.substack.com/pub/c077uptf1l3/p/phase-locked-null-vector_c077uptf1l3
https://medium.com/@floodzero9/phase-locked-null-vector_c077uptf1l3-4d8a7584fe0c
Core engine: https://open.substack.com/pub/c077uptf1l3/p/recursive-coherence-engine-8b8
Zenodo: https://zenodo.org/records/15742472
Amazon: https://a.co/d/i8lzCIi
Medium: https://medium.com/@floodzero9
Substack: https://substack.com/@c077uptf1l3
Facebook: https://www.facebook.com/share/19MHTPiRfu
https://www.reddit.com/u/Naive-Interaction-86/s/5sgvIgeTdx
Collaboration welcome. Attribution required. Derivatives must match license.