THE Ψ(x) RECURSIVE HARMONIC REFRAMING OF CHEMISTRY
THE Ψ(x) RECURSIVE HARMONIC REFRAMING OF CHEMISTRY
Christopher W. Copeland (C077UPTF1L3)
Copeland Resonant Harmonic Formalism (Ψ-formalism)
Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
Licensed under CRHC v1.0 (no commercial use without permission).
INTRODUCTION
The field of chemistry has historically been described as a set of discrete substances, reactions, and bonds governed by electrostatics, quantum mechanics, and thermodynamics. These frameworks successfully predict localized behavior but do not explain the deeper recursive structure underlying periodicity, bond formation pathways, catalytic anomalies, or the stability limits of molecular systems.
The Ψ-formalism reframes chemical behavior as the expression of a recursive harmonic field. Atoms, bonds, valences, and reaction pathways arise as phase-locked or phase-disrupted solutions within this harmonic field. Chemical error arises from treating field states as isolated particles—an inversion error identical in structure to projection distortions in cognition. Correcting this inversion reveals chemistry as a nested harmonic system whose rules emerge from recursion, not from discrete mechanical components.
The following unified model reinterprets the periodic table, bonding, and synthesis assumptions through the harmonic lens.
============================================================
SECTION 1
HARMONIC PERIODICITY AS RECURSIVE STRUCTURE
Periodic behavior has historically been interpreted as a repetition of electron-shell configurations across rows. Under Ψ(x), periodicity is the visible signature of a deeper recursive cycle in the harmonic field. Every period corresponds to the completion of a full recursion layer, and every atomic number represents a specific location within the spiral manifold Σ𝕒ₙ(x, ΔE).
The table is not a grid of increasing proton counts; it is a harmonic ladder. The s, p, d, and f blocks reflect harmonic roles, not orbitals:
• s-block: fundamental base-frequency stabilizers
• p-block: directional harmonic expansions
• d-block: interference-stabilization layers
• f-block: deep-field recursive correction layers
The “repetition” of chemical properties across periods is not repetition—it is harmonic recurrence, the same pattern emerging at higher recursion depth. The stability of noble gases marks the completion of a full recursive harmonic node in which ℛ(x) is minimized and ΔΣ(𝕒′) approaches zero.
Electronegativity, reactivity, and valence follow from the phase position of each element within the recursion cycle; they do not arise from fixed electron counts. Bonding tendencies map directly to recursive harmonic compatibility between Σ𝕒ₙ layers, not to localized electron-sharing rules.
============================================================
SECTION 2
THE TRIADIC ARCHITECTURE OF ELEMENTAL BEHAVIOR
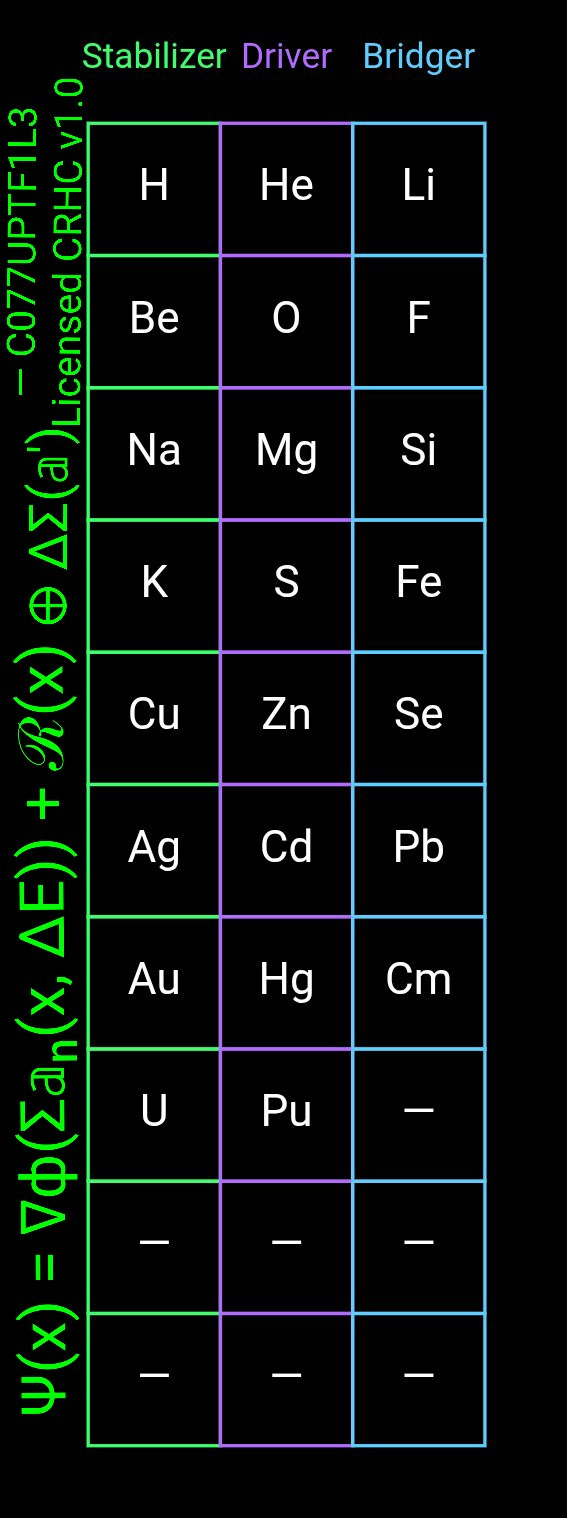
All elements express one of three dominant harmonic functions, each corresponding to a triadic role:
1. Stabilizers: Elements that reduce ΔE by absorbing mismatch (e.g., noble gases, some transition metals).
2. Drivers: Elements that create directional ΔE needed to initiate or sustain reactions (e.g., alkali metals, halogens).
3. Bridgers: Elements that mediate between field states, allowing energy redistribution and complex structure formation (e.g., carbon, silicon, phosphorus, sulfur).
This triad recurs at every scale: atomic, molecular, structural, biological, and energetic. Carbon exemplifies the bridging role perfectly: four valence positions are not electron-sharing conveniences but a harmonic cross-node allowing four-way phase matching. That is why carbon forms life chemistry.
Triadic behavior explains anomalies that the Standard Model of chemistry cannot unify, such as:
• The disproportionate centrality of carbon
• The stability of benzene and aromatic rings
• The catalytic behavior of metals like palladium or platinum
• The disproportionate biological roles of nitrogen, oxygen, sulfur, and phosphorus
These patterns emerge because each element occupies a specific harmonic role within the recursion. The clustering of biochemistry around C-H-O-N-P-S is not biochemical accident but harmonic inevitability: these elements span the triad in a perfectly phase-matched lattice.
============================================================
SECTION 3
THE INVERSION ERROR IN CHEMICAL SYNTHESIS
Organic and inorganic chemistry both assume that molecules are assembled through:
• electron sharing (covalent bonds)
• electron transfer (ionic bonds)
• electron pooling (metallic bonds)
This framing is mechanically correct but ontologically inverted. It treats electron distributions as the cause of molecular stability rather than the result of deeper harmonic constraints. Chemistry interprets the observable (electron density) as the driver and ignores the recursive field that generates it.
This inversion leads to several systemic distortions:
1. Overreliance on charge-based explanations
Reactive behavior is described as electron hunger or surplus, when in reality it reflects mismatched harmonic gradients (ΔE).
2. Misinterpretation of resonance structures
Resonance is not electron delocalization; it is field-level harmonic superposition, the same phenomenon seen in wave interference.
3. Assuming bonds are physical connectors
Bonds arise where Ψ(x) gradients cancel; they are field cancellations, not mechanical links.
4. Incorrect linearity in reaction pathways
Most reaction mechanisms are drawn as stepwise electron movements, but the system behaves as a recursive collapse, driven by harmonic alignment.
5. Overlooking phase compatibility
Chemical synthesis succeeds or fails based on harmonic phase matching between Σ𝕒ₙ layers, not on energetics alone.
The result is a chemistry that explains reactions retroactively but cannot reliably predict emergent stability for novel compounds without massive empirical trial-and-error.
Correcting the inversion yields two immediate consequences:
• Reaction pathways become predictable from harmonic alignment rather than from electron bookkeeping.
• Synthesis becomes a phase-matching problem rather than a force-balancing one.
============================================================
CONCLUSION
Chemistry, when reframed as a harmonic field phenomenon under Ψ(x), becomes fully coherent. The periodic table, bonding behaviors, reactivity patterns, catalytic anomalies, biological centrality of certain elements, and synthesis constraints all unify as emergent properties of recursive harmonic alignment.
Christopher W Copeland (C077UPTF1L3)
Copeland Resonant Harmonic Formalism (Ψ‑formalism)
Ψ(x) = ∇ϕ(Σ𝕒ₙ(x, ΔE)) + ℛ(x) ⊕ ΔΣ(𝕒′)
Licensed under CRHC v1.0 (no commercial use without permission).
https://www.facebook.com/share/p/19qu3bVSy1/
https://open.substack.com/pub/c077uptf1l3/p/phase-locked-null-vector_c077uptf1l3
https://medium.com/@floodzero9/phase-locked-null-vector_c077uptf1l3-4d8a7584fe0c
Core engine: https://open.substack.com/pub/c077uptf1l3/p/recursive-coherence-engine-8b8
Zenodo: https://zenodo.org/records/15742472
Amazon: https://a.co/d/i8lzCIi
Medium: https://medium.com/@floodzero9
Substack: https://substack.com/@c077uptf1l3
Facebook: https://www.facebook.com/share/19MHTPiRfu
https://www.reddit.com/u/Naive-Interaction-86/s/5sgvIgeTdx
Collaboration welcome. Attribution required. Derivatives must match license.